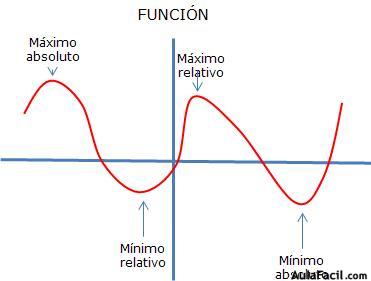
Máximos y Mínimos Relativos
Una función de dos variables tiene un máximo relativo en (a,b) si f(x,y) <= (a,b), cuando (x,y) está cerca de (a,b) el valor f (a,b) recibe el nombre de VALOR MAXIMO RELATIVO. Si cumple que f(x,y) >= (a,b) cuando (x,y) está cerca de (a,b) el valor de f(a,b) recibe el nomre de VALOR MINIMO RELATIVO. Si estas condiciones de desigualdad se cumplen en todo el dominio de f(x,y) entoncs toman el nombre de maximos y minimos absolutos.
TEOREMA: si f tiene un maximo o un minimo relativo en (a,b) las derivadas parciales de primer orden existen ahí, entonces fx(a,b) = fy(a,b) = 0.
Si la funcion de dos variables presenta un maximo relativo y un minimo relativo en un mismo punto, se dice que dicho punto es un PUNTO DE SILLA.
TEOREMA: si f tiene un maximo o un minimo relativo en (a,b) las derivadas parciales de primer orden existen ahí, entonces fx(a,b) = fy(a,b) = 0.
Si la funcion de dos variables presenta un maximo relativo y un minimo relativo en un mismo punto, se dice que dicho punto es un PUNTO DE SILLA.

No hay comentarios.:
Publicar un comentario